Выпуклый многоугольник. Теорема выпуклого многоугольника?
1 ответ:
Читайте также
Многоугольником в планиметрии (раздел геометрии, изучающий плоские фигуры) называется плоская фигура, которая образована замкнутым рядом прямолинейных отрезков. Эти отрезки являются сторонами многоугольника.
<hr />В зависимости от количества сторон, многоугольники называются:
треугольник [мн-к с 3-мя сторонами]
четырёхугольник [мн-к с 4-мя сторонами]
пятиугольник [мн-к с 5-ю сторонами]
и т. д.
<hr />Многоугольники бывают простые (на рис. слева) и звездчатые (на рис. справа):
Простые многоугольники не имееют самопересекаемых контуров; у зведчатых – контуры самопересекаются.
<hr />Многоугольники бывают выпуклые (на рис. слева) и невыпуклые (на рис. справа):
Все диагонали выпуклого многоугольника лежат внутри него, а у невыпуклого – диагональ (или диагонали) лежит вне многоугольника.
<hr />Многоугольники бывают вписанные в круг (на рис. слева) и описанные около круга (на рис. справа):
Все вершины вписанного в круг многоугольника лежат на окружности; все стороны описанного около круга многоугольника касаются окружности.
<hr />Правильный многоугольник имеет равные стороны и углы:
Правильный треугольник – это равносторонний треугольник; правильный четырёхугольник – квадрат.
Три отрезка, соединяющих вершины треугольника ABC (вершины обозначим как A,B и C) с некоторыми точками на противоположной стороне этого треугольника (соответственно это будут точки C1, A1 и B1 ), которые мы можем обозначить традиционно AA',BB',CC' проходят через одну точку или параллельны) тогда лишь, когда:
Доказательство на сайте ресолвента.ру
Справедлива теорема.
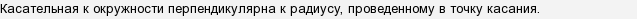
а - касательная, ОА - радиус окружности. Докажем, что ОА перпендикуляр к а.
Пусть радиус и касательная не перпендикулярны. Тогда ОВ - перпендикуляр. Но в этом случае ОА - наклонная и OA > OB, а т. В внутри круга. Поэтому прямая a и окружность имеют две общие точки, что противоречит условию ( а - касательная ). Отсюда следует, что касательная перпендикулярна к радиусу. Теорема доказана.