Просто- не просто, но здесь нужна простая- незамысловатая логика, чтобы рассуждать о чем- либо, чтобы доказать чего- то. Лежит что- то на полке, непонятно чье,то-ли ваше, то ли - сестры и для установления принадлежности, вы начинаете логически рассуждать, оценивая параметры вещи- содержание, цвет, размеры и пр. все сравнив и оценив, приходите к выводу,- не мое, потому что я
такое не купила бы ни в жизнь, значит- сестры, и когда это подтверждается, значит доказана она самая- теорема. А если есть железное доказательство принадлежности- например- подпись, то это уже- аксиома, та же теорема,не нуждающаяся в доказательствах. Если доказывается равенство треугольников, по
двум сторонам и углу между ними кто будет отрицать, что стороны совпадут при наложении. В общем, стараться надо, чтобы любовь к математике взаимной была,
( в противном случае- негатив до самого ЕГЭ.)

Справедлива теорема.
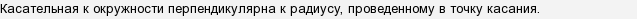
а - касательная, ОА - радиус окружности. Докажем, что ОА перпендикуляр к а.
Пусть радиус и касательная не перпендикулярны. Тогда ОВ - перпендикуляр. Но в этом случае ОА - наклонная и OA > OB, а т. В внутри круга. Поэтому прямая a и окружность имеют две общие точки, что противоречит условию ( а - касательная ). Отсюда следует, что касательная перпендикулярна к радиусу. Теорема доказана.
Расширенная теорема Фалеса звучит следующим образом:
"Если две прямые line1 и line2 пересечь параллельными прямыми, то отсеченные отрезки на прямых line1 и line2 будут соответственно пропорциональны друг другу".
В задаче рассматриваются точки на плоскости.
Теорема утверждает, что если есть 5 точек, никакие три из которых не лежат на одной прямой, то можно выбрать 4 точки, образующие выпуклый 4-угольник.
Известна также как теорема Эрдёша-Секереша о выпуклых 4-угольниках.
Названа так Эрдёшем потому, что решение этой задачи привело к тому, что его друг Секереш женился.
Нужно начертить треугольник АВС , где АВ = c , ВС = a , AC = b , углы же так и обозначим < A , < B , < C . Из вершины угла В опустим перпендикуляр ВД на АС , и обозначим его h. И рассмотрим треугольники АВД , и ВДС. Из них выведем соотношения : sin A = ВД /AB = h/c , sin C = ВД / ВС = h /a , Далее выведем соотношения для h , которое участвует в обоих равенствах:
h = c * sin A = a * sin C , откуда можно вывести часть теоремы синусов :
<h2>a / sin A = b / sin B .</h2>
Аналогично доказывается соотношение равенство для угла С :
<h2>A / sin A = c / sin C</h2>
И далее это равенство преобразуется в выражение теоремы синусов :
<h2>a / sin A = b / sin B = c / sin C = 2R</h2>
Если рассматривать этот треугольник в описанной окружности,то там учитывается радиус описанной окружности R.