Однозначно геометрия! Там всё просто и интересно! Фигуры, графики, теоремы и аксиомы! мне очень в школе это нравилось. предмет давался легко, с удовольствием всё делала и отлично получалось. Но алгебра, ...были такие темы, что даже теперь по ночам снится контрольная по алгебре, время на исходе, а у меня в тетради одно условие..Жуть!
Каждый школьник и взрослый знаком с задачами по математике, где есть такое условие: "Из пункта А в пункт Б отправляется..." Почему все поезда из математических задач едут из пункта А в пункт Б? Ответ на этот вопрос прост.
Пункт А и пункт Б — это всего лишь условное обозначение расстояния между двумя странами, городами или улицами, например. Перечислять можно до бесконечности. Не стоит изобретать велосипед там, где это не нужно. Поезд может быть заменен другим транспортным средством- автомобилем или мотоциклом, оно не играет здесь ключевой роли. Такие математические задачи дают детям в школе, чтобы развить их абстрактное мышление. Условие задач может быть разным: узнать скорость поезда, время его прибытия в пункт назначения и так далее. Кроме того, поезд может ехать не только из пункта А в пункт Б, два поезда могут двигаться навстречу друг другу. Цель таких задач одна - выяснить, решить что-то, и совершенно не важно как называются эти пункты, А и Б, В и Г или Д и Е. Буквы А и Б для обозначения пунктов выбраны, я считаю, только потому, что это - первые буквы алфавита, не более того.
Может такой проект и будет иметь место, ведь нужно обратить внимание на то, что некоторые дети потенциально не понимают азов математики, на уровне +- поделить и умножить ещё куда ни шло, а вот дроби, уравнения, ну ни в зуб ногой. И может оно и к лучшему, ведь зачем заставлять углублённо изучать математику того, кто станет отличным автомехаником, или филологом.
Каждому своё и право выбора, это здорово, значит можно будет углубиться в другие предметы.
Прямоугольный параллелепипед показан на рисунке.
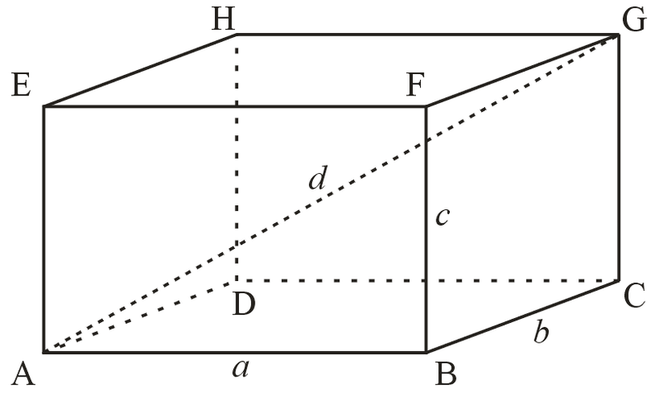
Имеем b = 6 м, а = 8 м и с = 10м. Найти угол между диагональю параллелепипеда d =AG и плоскостью его основания ABCD, то есть угол между диагоналями AG и АС. (На рисунке диагональ АС не нарисована). Вначале найдем длину диагонали АС = sqrt(a^2 + b^2) = sqrt(8^2 + 6^2) = sqrt(64 + 36) = sqrt(100) = 10 м. (На рисунке диагональ АС не прочерчена, на своем рисунке прочертите ее для наглядности). Значок sqrt означает квадратный корень (от английских слов square root). Математический знак корня БВ не понимает, поэтому ставит вместо него знак вопроса ?). БВ не понимает ни греческие буквы, ни математические знаки, которых нет на клавиатуре. Итак, АС = 10 м. Имеем прямоугольный треугольник АСG. Теперь легко найти угол CAG в этом треугольнике CAG. Угол GCA будет прямоугольным (90°), так как ребро GC в параллелепипеде перпендикулярно основанию ADCB. Из прямоугольного треугольника AGC находим тангенс угла GAC. При этом заметим, GC = с = 10 м, так как оба эти катета – высота параллелепипеда. Имеем tg(GAC) = GC/AC = 10/10 = 1. А если тангенс равен 1, то это угол в 45°. Ответ 45°.
Так как в условии высота( образующая в прямом ц.является высотой) меньше диаметра, делаем вывод, что высота два корня из пяти. Тогда 10 корней из 5- длинна окружности основания ц. Длина окружности равна два пи на радиус. Отсюда находим радиус. Он будет пять корней из трех деленные на пи. Получаются числа с корнями и пи. Если хотите неточные цыфры, можно подставить пи и вывести из под корня. Но мамематика любит точность, поэтому решение такое