Задача решаемая, и я решил!)
Приступим!
z^2>=0, так как квадрат числа всегда положительный, или равен 0.
xy-z^2=1 - отсюда следует, что xy>=1
xy>=1 отсюда следует что либо x и y либо оба положительны, либо оба отрицательны, но по скольку мы знаем что x+y=2 следует, что и x и y положительные числа, так как из суммы отрицательных чисел, положительное число 2 никак не получиться. У нас появилась новая система уравнений, неравенств. - xy>=1; x+y=2; x>0; y>0, z пока оставим в покое. Отбросим пока x>0; y>0, и решим систему уравнений, неравенств - xy>=1; x+y=2. xy>=1 это тоже самое что y>=1/x, отсюда можно сделать функцию y=1/x - график данной функции - стандартная гипербола. А x+y=2 это тоже самое что y=2-x -стандартная линейная функция поднятая на 2 единицы вверх и перевернутая. Я Сделал себе рисунок этих графиков, что бы понять, что они пересекаются всего в 1й или 2х точках.
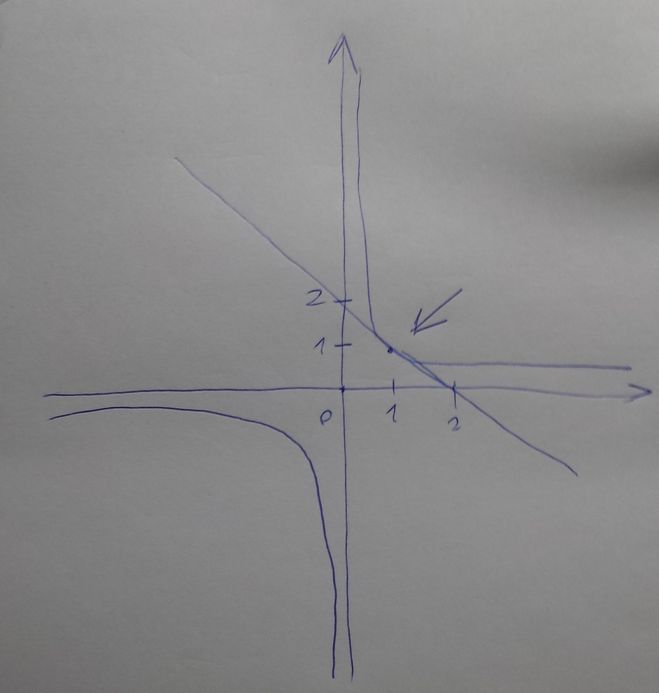
Теперь уже неравенство нам не нужно и мы переходим к системе уравнений, что бы вычислить данную точку - y=2-x;y=1/x - данную систему уравнений уже просто решить - 2-x=1/x отсюда следует, что x(2-x)=1 следовательно -x^2+2x-1=0 стандартное квадратное уравнение (мог расписать его решение, но мне лень), корень которого x=1, корень тут всего 1 оказался.
Значение x мы знаем теперь подставляем его в x+y=2, следовательно 1+y=2 отсюда следует, что y=1. Теперь зная x и y можно без труда вычислить z - xy-z^2=1 следовательно z^2=0 а следовательно z=0. Вот вам и решение x=1 y=1 z=0.
Наверное, не как доказать, а как найти решение уравнения в натуральных числах.
2000х+513у=2513
2000х-2000=513-513у
2000(х-1)=513(1-у)
Поскольку х и у - натуральные числа, то из последнего равенства следует что х=у=1,иначе получается что левая и правая части имеют разные знаки.
Для решения этого уравнения достаточно 204 умножить на 59.
Вообще, любой подобное уравнение решается достаточно просто, методом треугольника: представьте себе в виде треугольника три цифры: одна цифра в верхнем углу треугольника и две цифры расположены по нижним углам. В верхнем углу - результат произведения умножаемого и множителя, расположенных в двух нижних углах. Закрыв рукой неизвестное - у нас на картинке сразу появится необходимое действие, для нахождения неизвестного.
На картинке отображен треугольник в виде закона Ома.
Чтобы найти V нам необходимо перемножить I и R. Чтобы найти R нам необходимо разделить V на I.
Сделаем некоторые преобразования вашего уравнения. Здесь значок ^ означает возведение в степень.
x^3 – 6x^2 – 4x + 24 = x^3 – 4x + 24 – 6x^2 = x(x^2 – 4) – 6(x^2 – 4) = (x^2 – 4)(x – 6) = 0. Если любой из этих сомножителей равен нулю, то и всё произведение равно нулю.
Поэтому (1) x^2 – 4 = 0. Тогда х^2 = 4. То есть х в квадрате равно 4. Отсюда имеем два решения для х. х = 2 и х = -2.
И (2) x – 6 = 0. Отсюда х = 6.
Итак, имеем 3 ответа. х = 2, х = -2 и х = 6. И из алгебры известно, что уравнение 3-й степени имеет 3 решения.
x^3=-18-5x. В левой части функция возрастающая, в правой части убывающая. Следовательно корень, если он есть, единственный . Подбором находим, что единственное решение х=-2. Для проверки можно ещё построить два графика у=х^3 и у= - 18-5х. Эти графики будут иметь единственную точку пересечения ( х=-2, у=-8)