Question

Решите систему уравнений: x+y=2; xy-z^2=1?

Answer 1

Задача решаемая, и я решил!)

Приступим!

z^2>=0, так как квадрат числа всегда положительный, или равен 0.

xy-z^2=1 - отсюда следует, что xy>=1

xy>=1 отсюда следует что либо x и y либо оба положительны, либо оба отрицательны, но по скольку мы знаем что x+y=2 следует, что и x и y положительные числа, так как из суммы отрицательных чисел, положительное число 2 никак не получиться. У нас появилась новая система уравнений, неравенств. - xy>=1; x+y=2; x>0; y>0, z пока оставим в покое. Отбросим пока x>0; y>0, и решим систему уравнений, неравенств - xy>=1; x+y=2. xy>=1 это тоже самое что y>=1/x, отсюда можно сделать функцию y=1/x - график данной функции - стандартная гипербола. А x+y=2 это тоже самое что y=2-x -стандартная линейная функция поднятая на 2 единицы вверх и перевернутая. Я Сделал себе рисунок этих графиков, что бы понять, что они пересекаются всего в 1й или 2х точках.

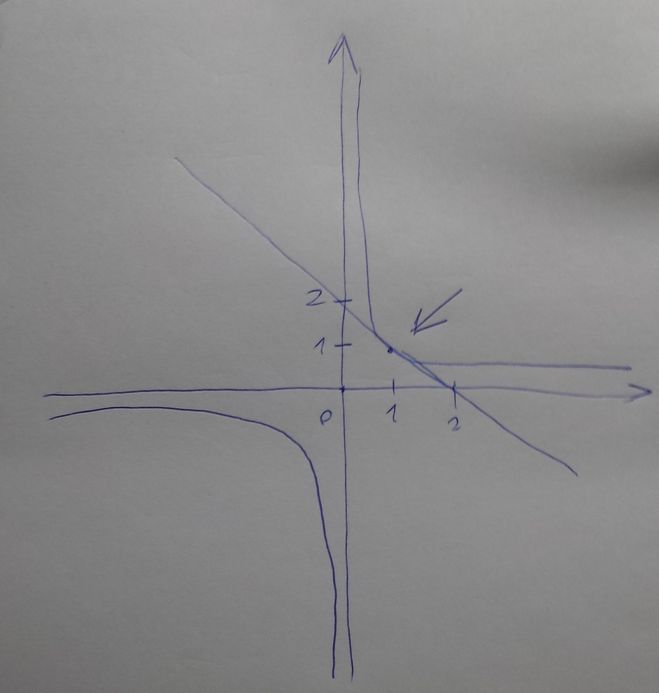
Теперь уже неравенство нам не нужно и мы переходим к системе уравнений, что бы вычислить данную точку - y=2-x;y=1/x - данную систему уравнений уже просто решить - 2-x=1/x отсюда следует, что x(2-x)=1 следовательно -x^2+2x-1=0 стандартное квадратное уравнение (мог расписать его решение, но мне лень), корень которого x=1, корень тут всего 1 оказался.

Значение x мы знаем теперь подставляем его в x+y=2, следовательно 1+y=2 отсюда следует, что y=1. Теперь зная x и y можно без труда вычислить z - xy-z^2=1 следовательно z^2=0 а следовательно z=0. Вот вам и решение x=1 y=1 z=0.

Answer 2

Можно решить несколько проще. Пусть х и у - корни квадратного уравнения (относительно t).

Тогда по теореме Виетта, должно быть t^2-2*t+(z^2+1)=0.

Его решения: t(1,2)=(1+-)√(1-z^2-1)=1(+-)√(-z^2).

Так как (-z^2) должно быть неотрицательным, то в действительных числах z=0, и t(1)=t(2)=1.

А так как t(1)=х, t(2)=у, получаем х=1, у=1.

Итак единственное решение: х=1, у=1, z=0.

Answer 3

Сразу замечаем, что в системе уравнений два уравнения и три неизвестных, следовательно однозначного решения мы не получим. Данная система будет иметь бесконечно много решений, т.к. какие бы две переменные мы не выразили третья останется и будет задавать разнообразие решений. Казалось бы систему можно не решать, но попробуем совершить некоторые преобразования. Вдруг получится что-нибудь "красивое".

Итак имеем два уравнения:

1) x+y=2;

2) xy-z^2=1

Возведём в первом уравнении обе части в квадрат

1) x^2+2xy+y^2=4;

2) xy-z^2=1

Поделим первое уравнение на 2

1) x^2/2+xy+y^2/2=2;

2) xy-z^2=1

Теперь из первого уравнения вычтем второе. Имеем:

x^2/2+y^2/2+z^2=1 (*)

Уравнение вида (*) ни что иное, как каноническое уравнение второго порядка, описывающее эллипсоид.

Можем заключить, что все решения данной системы лежат на эллипсоиде с полуосями a=sqrt(2), b=sqrt(2), c=1, sqrt - квадратный корень.

Answer 4

А можно и аналитически решить, не применяя графиков. Выразим из первого уравнения y=x-2. Подставим во второе, тогда получим:

x(2-x)-z^2=1

2x-x^2-z^2=1

-x^2-z^2=1-2x

x^2+z^2=2x-1

z^2=-x^2+2x-1

Данное равенство будет верным в том и только в том случае, когда правая часть неотрицательна, то есть:

-x^2+2x-1>=0

x^2-2x+1<=0

(x-1)^1<=0

А это справедливо, если x=1.

Тогда отсюда z=-1^2+2*1-1=-1+2-1=0

А y=2-1=1.

Мне кажется, что так гораздо проще. И особой фантазии не надо.