sin^2(x)-2*sin(x)*cos(x)=3*cos^2(x) (1),
sin^2(x)-2*sin(x)*cos(x)-3*cos^2(x)=0 (2)
Убеждаемся, что cos(x) не может равняться нулю. Допустим, что cos(x)=0. Подставив это значение в уравнение (2) получим sin(x)=0. Но и синус и косинус одного и того же угла не могут одновременно равняться нулю. Значит наше допущение что cos(x)=0, было неверным. Такого рода проверка является ОБЯЗАТЕЛЬНЫМ ЭЛЕМЕНТОМ РЕШЕНИЯ ЛЮБЫХ УРАВНЕНИЙ, если мы решили разделить все члены уравнения (или неравенства) на какое-либо выражение, содержащее неизвестное.
Значит cos(x) не равен нулю. Тогда мы имеем право все члены уравнения (2) поделить на cos(x)^2. Получаем:
tg^2(x)-2tg(x)-3=0 (3).
Получилось простое уравнение второй степени (квадратное) относительно tg(x).
Его решения tg(x)=-1 и tg(x)=3.
Окончательно x(1)= -Пи/4 + Пи*k, где k - любое целое число.
Аналогично x(2)= arctg(3) + Пи*k, где k - любое целое число.
<hr />
NataLi! Позвольте дать Вам один хороший совет. Когда Вы обращаетесь с подобными просьбами, не пишите свою просьбу в приказном тоне "Требуется...". Это очень плохо воспринимается и отталкивает потенциальных помощников. Лучше написать так "Пожалуйста, приведите...".
Для третьеклассников возможно такое решение этого уравнения или числового равенства. Понятно, что можно получить ответ в такой форме 7-2 =5. То есть первую "семерку" оставляем, из трех оставшихся "7" нужно получить "2". И тут подсказка есть 14:7=2. Значит остается получить 14 из двух "7", что совсем просто. Ответ такой: 7 - (7 + 7) : 7 = 5
Опять как "а у какой звезды?" , встаёт вопрос "а какое именно кубическое уравнение?"
x^3 = 0 решили сразу, как только до него додумались. Наверно ещё египтяне до строительства пирамиды Хеопса. Понятие объёма им точно было знакомо.
x^3 = 1 полноценно смогли решить, только осознав необходимость использования комплексных чисел. Первые намёки на комплексные числа появились в книге «Великое искусство, или об алгебраических правилах» Кардано (1545)
Хотя решение кубических уравнений по утверждению самого Кардано он позаимствовал у Николло Тарталья, а тот в свою очередь у Сципиона дель Форто, говорить о полном решении кубического уравнения в общем виде, когда фигурирует только действительный корень, как-то не вполне корректно.
А вот решение уравнения четвёртой степени в общем виде уже однозначно заслуга Кардано и его ученика Феррари (авторы легко запоминаются, как "кардан от «Ferrari»")
Есть ещё один нюанс. В действительных числах можно решать и численными методами. Ко времени опубликования работ по аналитическому решению уравнений третьей и четвёртой степени, численные методы были уже настолько развиты, что трудоёмкость аналитического решения иногда превышала приближённые вычисления корня.
Давненько, лет 40 не решал дифференциальные уравнения, многое забыл, кажется решать нужно примерно так, но кое-что мог и упустить.
dy/dx=2y-3.
dy/(2y-3)=dx,
(1/2)*d(2y-3)/(2y-3)=dx,
d(2y-3)/(2y-3)=2dx
ln(2y-3)+lnC=2x,
ln(C*(2y-3))=2x,
C*(2y-3)=e^(2x),
2y-3=(1/C)*e^(2x),
2y=3+(1/C)*e^(2x),
y=1,5 +(e^(2x))/(2*C).
Задача решаемая, и я решил!)
Приступим!
z^2>=0, так как квадрат числа всегда положительный, или равен 0.
xy-z^2=1 - отсюда следует, что xy>=1
xy>=1 отсюда следует что либо x и y либо оба положительны, либо оба отрицательны, но по скольку мы знаем что x+y=2 следует, что и x и y положительные числа, так как из суммы отрицательных чисел, положительное число 2 никак не получиться. У нас появилась новая система уравнений, неравенств. - xy>=1; x+y=2; x>0; y>0, z пока оставим в покое. Отбросим пока x>0; y>0, и решим систему уравнений, неравенств - xy>=1; x+y=2. xy>=1 это тоже самое что y>=1/x, отсюда можно сделать функцию y=1/x - график данной функции - стандартная гипербола. А x+y=2 это тоже самое что y=2-x -стандартная линейная функция поднятая на 2 единицы вверх и перевернутая. Я Сделал себе рисунок этих графиков, что бы понять, что они пересекаются всего в 1й или 2х точках.
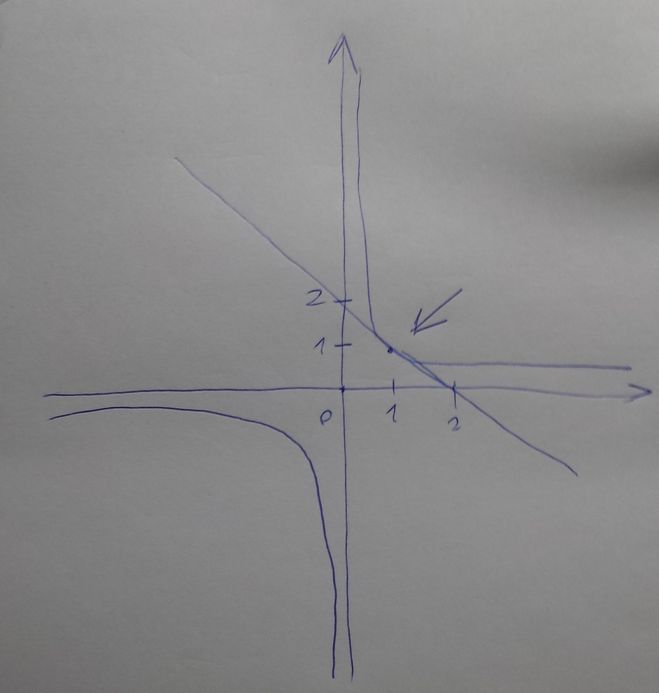
Теперь уже неравенство нам не нужно и мы переходим к системе уравнений, что бы вычислить данную точку - y=2-x;y=1/x - данную систему уравнений уже просто решить - 2-x=1/x отсюда следует, что x(2-x)=1 следовательно -x^2+2x-1=0 стандартное квадратное уравнение (мог расписать его решение, но мне лень), корень которого x=1, корень тут всего 1 оказался.
Значение x мы знаем теперь подставляем его в x+y=2, следовательно 1+y=2 отсюда следует, что y=1. Теперь зная x и y можно без труда вычислить z - xy-z^2=1 следовательно z^2=0 а следовательно z=0. Вот вам и решение x=1 y=1 z=0.