Представим искомое двузначное число как (10х + у), где х и у - натуральные однозначные числа.
Составляем уравнение:
10х + у = 2ху.
Очевидно, что решить его нам не удастся без подстановок цифр на место х. Подставляем цифру 1. Тогда
10 + у = 2у
10 = 2у - у
у = 10.
По условиям не подходит, так как и икс, и игрек должны быть однозначными. Берём х = 2.
20 + у = 4у
20 = 4у - у
3у = 20
у = 20 6 3 = 6,(6).
Тоже не подходит, потому что по условиям х и у должны быть натуральными числами.
Подставляем 3.
30 + у = 6у
30 = 6у - у
5у = 30
у = 6
Итак, это 36. Произведение 3 и 6 даёт 18, что ровно в 2 раза меньше 36.
Есть стихотворения и фразы (иногда довольно забавные, а также длинные), в которых зашифровано множество знаков числа "пи". Причем на разных языках. На русском:

До 1918 года можно было воспользоваться фразой:
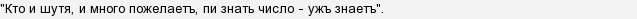
Парочка на английском:

А вот еще лучше:

Есть на французском, немецком и других языках. В некоторые фразы авторы умудрились загнать не только имя Пифагора, но и название его города Сиракузы!

(Придумано не позднее 1906 года.)
А) АААВВС - это число вида 999887, очевидно, что при этом комплекте цифр оно может быть самым большим
Б) САААВВ - число вида 988877, тоже явно может
В) ВВАААС - число вида 998887, может
С) АААВСВ - это 1) число вида 999878, но из этого же комплекта цифр мы можем составить большее: 999887, или 2) число вида 999787, но оно меньше, чем 999877 из того же комплекта
Д) АААСВВ - число вида 999877, может быть самым большим
Таким образом, правильный ответ С (Г?) АААВСВ
При решении этой задачи не нужно присваивать определённым буквам определённые цифры и пытаться сравнивать ответы между собой)
2 Пи = 6,28318530718.
Среди математиков ведутся разговоры о том, что следует заменить число Пи числом Тау. Что это значит? С точки зрения математиков числом Пи неудобно пользоваться. Гораздо комфортнее, по их мнению, пользоваться другой математической константой – числом Тау. Это число выражает отношение длины окружности к ее радиусу. Величина Тау в 2 раза больше числа Пи, т.е. если последнее равно 3,14, то Тау 6,28. Естественно, значение приблизительно.
Четырёхзначных чисел, составленных из нечётных цифр, существует 625 штук.
Нечётных четырёхзначных чисел существует гораздо больше - 4500 штук.
Вычисляется достатачно просто - нужно перемножить количества вариантов для каждой цифры числа.