В очередной раз, проводя ревизию в своих вопросах, на которых можно получить «Реставратора», я обратил внимание на это задание. С виду совсем не сложное. По крайней мере выдать хоть какую-то версию не составляет никакого труда. Ведь можно элементарно выяснить ширину и высоту банкноты. Сведения о ней хранятся на сайте ЦентроБанка Российской Федерации - ширина равна 69мм, а длина = 157мм. Там же для каждой из выпускаемых монет можно узнать соответствующий диаметр: 1руб = 20,5мм; 2руб = 23мм; 5руб = 25мм; 10руб = 22мм и для биметаллической памятных десятирублёвок диаметр = 27мм. Полученные данные я занёс в табличку, а заодно вычислил радиусы монет, поделив их диаметры пополам:
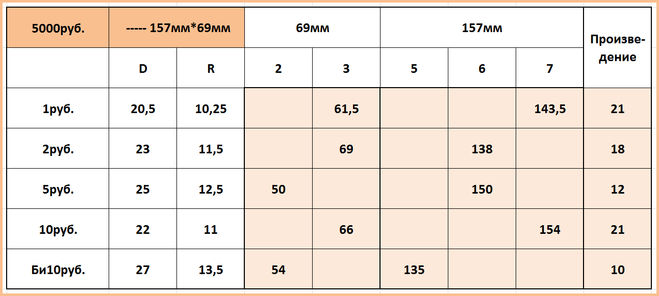
Если ширину купюры (69мм) разделить на диаметр рублёвой монеты (20,5мм), мы получим три «с хвостиком». Это означает, что в ширину можно выложить три монетки. они займут 61,5мм. Маленьких «червонцев» поместится тоже три и останется чуть меньше места. А двухрублёвые на удивление улягутся плотно - 3 * 23мм = 69мм. Пятаков и больших десяток ляжет только по две. Если же выкладывать монеты по длинной стороне пятитысячной банкноты, то там при каждом делении остаётся дробная часть и ни один из видов монет плотно не ляжет. Это хорошо видно на примере двух рублей:
Три по одной стороне, шесть целых монет по другой стороне - 3 * 6 = 18 монет. В нашей таблице это число записано в колонке «Произведение». Для каждой монеты посчитано. Но, может быть, следует поменять способ укладки и сдвинуть монеты в половине рядов на длину их радиуса? Ведь хотя бы в некоторых местах круглые денежки лягут плотнее. Давайте попробуем проделать такую операцию вручную:
Кажется странным, но мы получили те же 18 целых монет, а подрезанных их даже на одну меньше - всего две. Видимо, при таких соотношениях сторон «длина/ширина/диамет<wbr />р» нам не удастся добиться лучших результатов. Может быть, если взять листок побольше, а монеты помельче, доля пустот сократилась бы. Но это очень муторное дело - брать огромную газету и выкладывать на ней копеечные монетки. Нет ли какого-нибудь теоретического способа вычисления? Наверняка есть. И, ещё раз подумав, я взял рублёвые - самые маленькие монетки.
Положив по две в ряд, я заметил, что добавление каждого следующего ряда будет сокращать оставшуюся длину банкноты на одинаковое значение, которое больше радиуса, но меньше диаметра монеты. Если равно диаметру, монеты укладываются плотно, как в случае в двух-рублёвками. Есть предложение пока отрезать лишнее и перевернуть оставшуюся часть картинки для удобства наблюдения:

Увидев полученную картинку, я сперва содрогнулся - неужели придётся разбираться с синусами и косинусами? И ведь бросать-то не хочется, потому что уже столько сил и времени потрачено. И тут мне пришло в голову разобраться со «щелями» - теми расстояниями, что участвуют в расчётах, помимо диаметров и радиусов монет. Я провёл две линии - вертикальную и горизонтальную, а на них сделал отметки, отсекающие радиусы. Выяснилось, что у нас всего две неизвестных пока величины, которые мы назовём «y» и «x». Причём, вторую можно вычислить без особого труда, потому что ширина банкноты равна 69мм, а радиус рублёвой монеты мы вычислили в самом начале = 10,25мм.
В таком случае мы имеем:
- R + R + x + x + R + R + x + R = 69
- 5R + 3x = 69
- 3x = 69 - 5*10,25 = 17,75
- x = 17,75 / 3 = 5,916 (и 6 в периоде)
А как вычислить «y»? Ведь нам как раз и нужна эта величина, чтобы узнать, на какое расстояние продвигается вперёд каждый следующий слой монет? И тут мне пришло в голову опустить в параллелограмме высоту, получив прямоугольный треугольник:
И тут не надо никаких синусов. Нам достаточно помянуть добрым словом Пифагора, потому что для выделенного треугольника справедлива следующая формула (квадрат гипотенузы равен сумме квадратов катетов):
- (R+y)² + (R+x)² = D²
- (R+y)² = D² - (R+x)²
- R+y = Корень(D² - (R+x)²)
- y = Корень(D² - (R+x)²) - R = 2,355113601
И теперь остаётся сказать, что после первого слоя с высотой «D» каждый следующий будет сокращать оставшуюся длину банкноты на расстояние
- R+y = 10,25 + 2,355113601 = 12,605113601
Если длина купюры = 157мм, а высота первого слоя = 20,5мм, оставшаяся часть = 136,5мм. Это значение и следует разделить на полученное число 12,605113601:
- (157 - 20,5) / 12,605113601 = 136,5 / 12,605113601 = 10,8289385
Таким образом мы можем поместить на купюре в 5000 рублей 11 рядов рублёвых монет по 2 в каждом. Получается 11 * 2 = 22, что на одну больше, чем при выстраивании прямоугольника 7 на 3. Не существенная, но разница присутствует. И она, кстати, имеет место для номиналов 1, 5 и Би10 рублей (сравниваем строчки «Произведение» и «Всего монет»):
И только для маленьких монет по 10 рублей почему-то поместилось меньше. Где-то ошибка? Конечно, потому что кружочки надо располагать не по 2, а по три в ряд. Тогда потребуется немного изменить формулы и поместится чуть больше. Хотя, практика показывает, что для десяток мы ничего не выиграем - те же 21 целая монета. Ничего не сэкономили.
Вот, примерно так. Таким образом можно определить, удастся ли разместить круглые элементы на прямоугольном участке более плотно или нет. В некоторых случаях получается. В нашей задаче три эксперимента из пяти оказались удачными.