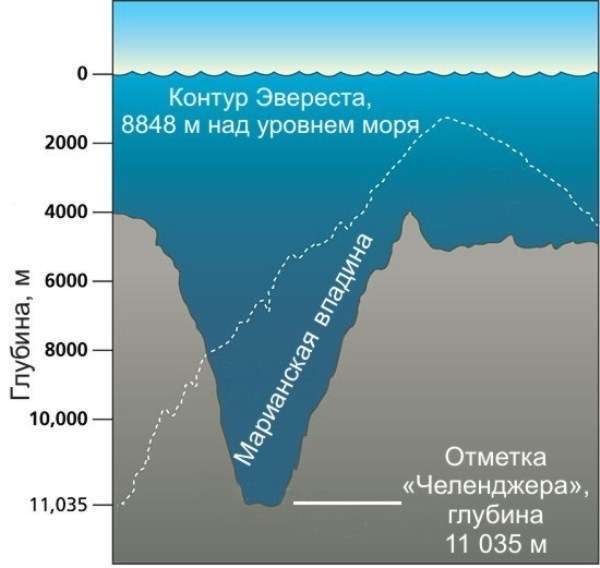
Ох, уважаемый Остап, не хотелось быть мне "добросовестным девятиклассником", но Вы, все же, уговорили меня. Поскольку задан вопрос о весе на дне Марианской впадины, то именно это и буду рассматривать. Во-первых, совершенно прав binom, утверждая, что вес будет зависеть от географического местоположения взвешиваемого тела. На полюсах тело будет тяжелее, чем на экваторе. Что касается района Марианской впадины, то вряд ли мы сможем найти достаточно точное значение g для этого места. Поэтому, на мой взгляд, совершенно не важно её географическое положение, и достаточно найти как изменится вес тела на дне в сравнении с весом на уровне моря в этом же месте Земли. Как верно подметил Владимир, задача, действительно чисто теоретическая, поскольку, естественно, ни кто не будет нырять на дно Марианской впадины, что бы взвесить кусок золота. Но теоретическая она не потому, что плотность Земли не постоянна, и что форма Земли геоид. Влияние флуктуаций упомянутых факторов в масштабе Земли настолько невелико, что о них не стоит и говорить. Так, например, если с Земли удалить весь мировой океан, масса которого, естественно учитывалась при определении средней плотности Земли, то средняя плотность Земли, как показывают расчеты, возрастет менее чем на одну десятую процента. Так что допустив , что плотность Земли постоянна в объеме Земли, мы не сделаем большой ошибки. И, полагаю, погрешность вычисления изменения веса будет значительно меньше 10 %. Думаю, эта погрешность будет существенно меньше одной десятой процента. Если тело, не находящееся в воде, неподвижно в вертикальном направлении или его скорость в этом направлении постоянна, то вес тела будет численно равен гравитационному взаимодействию между этим телом и Землей, за вычетом выталкивающей силы атмосферы. Впрочем Архимедова сила атмосфера для золота настолько ничтожна, что в дальнейших рассуждениях о ней можно забыть. На какой-либо глубине (Н) в толще земли или в водах мирового океана сумма гравитационных сил действующих на тело со стороны слоев земли и воды лежащих выше радиуса (r) определяемого выражением r = Rз - H (где Rз - средний радиус Земли), будет равна нулю. Т.е. для тела находящегося на расстоянии r от центра Земли, слоев земли и воды, лежащих выше, как бы и не существует. Таким образом, отношение веса тела на уровне моря к весу тела находящегося на расстоянии r от цента Земли будет равно (из закона всемирного тяготения) r^2 Мз/ Rз^2 mз. Здесь Мз -масса всей Земли; mз - масса объема Земли с радиусом r. Выразим эти массы через объем и среднюю плотность Земли. Тогда отношение веса тела на уровне моря к весу тела находящегося на расстоянии r от цента Земли будет равно Rз/r. Таким образом, тело находящееся ниже уровня моря за счет уменьшения силы гравитации будет весить меньше, чем на уровне моря. Но наше тело находится на дне океана, а значит на него ДЕЙСТВУЕТ Архимедова сила. И вес тела еще уменьшится на величину равную весу вытесненной морской воды. Выразив вес тела через его объем и плотность, а вес вытесненной воды через объем тела и плотность воды на глубине 11 км, можно определить, что отношение веса тела на глубине 11 км, но не в воде, к весу тела на этой же глубине в воде равно Пт/(Пт - Пв); где Пт - плотность тела; Пв - плотность воды на глубине 11 км. Окончательно имеем, что вес тела на дне Марианской впадины будет меньше веса этого тела на уровне моря (не в воде) в RзПт/r(Пт - Пв) раз. Подставив числовые значения определим, что кусок золота на дне Марианской впадины будет весить в 6371 * 19,32/6360*( 19,32 - 1,076) = 1,06081 раза меньше, чем на уровне моря.
Что касается Луны, то её гравитационное воздействие на кусок золота, минимум в 294260 раз меньше гравитационного влияния Земли. Так стоит ли его учитывать? При желании, конечно, можно учесть и это влияние.